Generative Adversarial Nets for High-dimensional Mean Field Games
Overview
There are two generative models in the data generation business right now: Generative Adversarial Nets (GAN) and Variational Autoencoder (VAE). These two models have different take on how the models are trained. GAN is rooted in game theory, its objective is to find the Nash Equilibrium between discriminator net and generator net. On the other hand, VAE is rooted in bayesian inference, i.e. it wants to model the underlying probability distribution of data so that it could sample new data from that distribution.
In this work, we use GAN to solve high-dimensional mean field games (MFGs), which are beyond reach with existing solution methods. In particular, the MFG is represented by two partial differential equations. The generator and discriminator are used to approximate them, respectively.
A glimpse of experiment
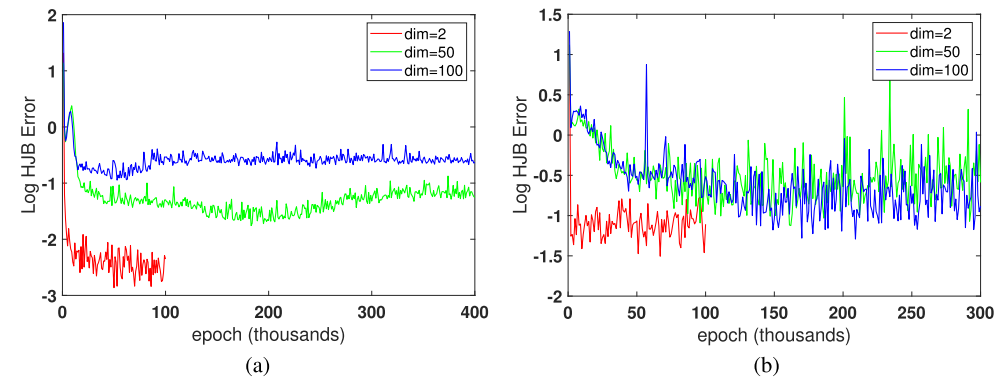
Convergence of training at different dimensions
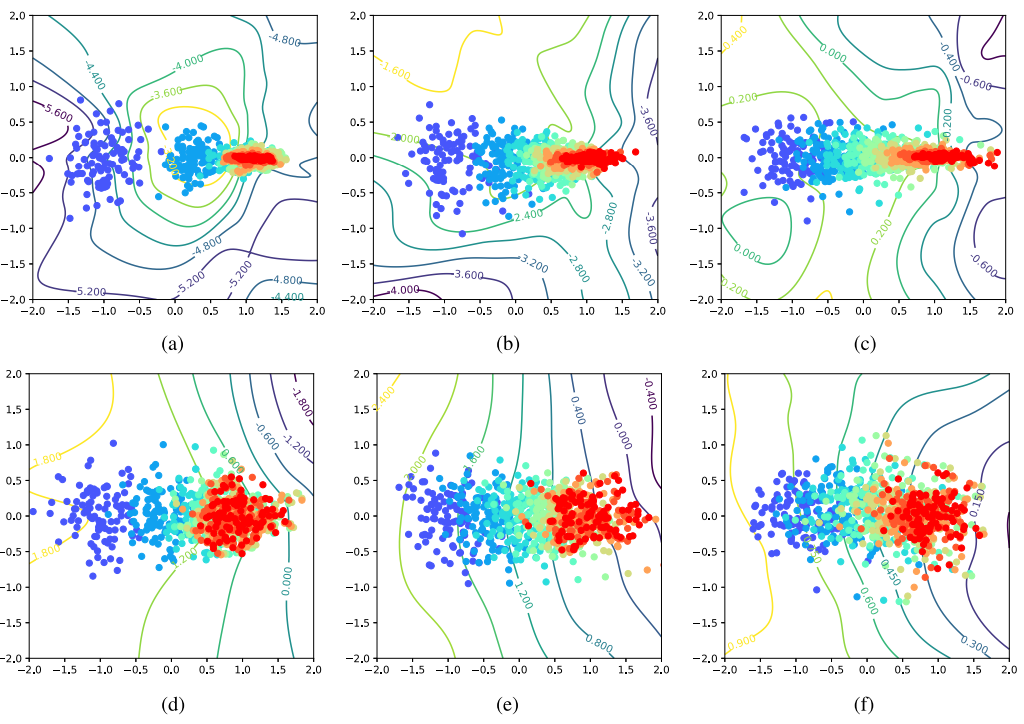
Diffusion of mean field
Each point represents a player and different color represents different time slots.
Code
- Apac-net at Github
- Programming: Python
- ML Framework: PyTorch
Publication
- H. Gao et al., “Opinion Evolution in Social Networks: Connecting Mean Field Games to Generative Adversarial Nets,” in IEEE Transactions on Network Science and Engineering.
